In praise of composition: knot groups and cospans
I have been thinking about knots recently. The context is our work (with Sabadini, Katis, Rosebrugh etc) since 1997 ([1]) in using the tensor and composition in categories of spans and cospans to describe "evolving nets of automata" - the most recent paper being [4]. After these thoughts I noticed that the main idea of this post, seen somewhat differently, has already been discovered by John Armstrong (see below). It could easily be also in other works, for example Yetter's book on Functorial Knot Theory (I don't have a copy).
The idea is to see a knot as a system composed from parts. Let's look at the trefoil:
The components which we wish to use to build knots are the following:
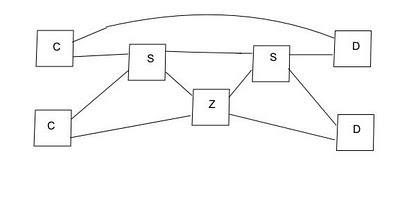
I am going to call these components C, Z, S and D respectively (chosen for a vague resemblance with the geometry). If I draw these as boxes rather than wires I get a picture for the trefoil that looks like a circuit diagram:
Now to calculate the knot group of the trefoil we label all the edges of the circuit with distinct letters, and the components with equations which relate the letters on the adjacent wires with the following result:
By looking at particular C,D,Z,and S components in this picture one can see the rule for assigning equations.
Finally, the knot group is the free group on all the letters quotiented by the equations.
In the case of the trefoil, if we express all the letters in terms of "a" and "e" the equations reduce to one equation, namely "aea=eae", so the knot group is ‹ a,e; aea=eae› .
Notice the resemblance to, for example, analogue circuit diagrams where we associate voltages and currents to the wires and differential equations to the components (see [3,4])
So what are we doing here? The letters on the wires entering (or leaving a component) may be thought of as the generators of a free group. The equation in the middle of a component may be thought of a the quotient of the coproduct of the input and output free groups defined by the relations. So a component is a cospan of groups between free groups. The whole diagram is a tensor diagram in Groups (the tensor being +) and the knot group is its tensor colimit as described in [2]. As described in [2] this colimit may be calculated by evaluating an expression in the monoidal category of cospans of groups.
For the trefoil, the expression is (C+C)*(1+S+1)*(1+1+Z)*(1+S+1)*(D+D) (+ means coproduct, * means composition).
Notice that a cospan of groups is assigned to any meaningful expression, that is to any tangle, not just to closed knots. The cospan corresponding to a braid is Artin's representation of a braid as an automorphism of a free group.
One of the motives for these thoughts were the remarks I made in an earlier post that graphical languages should be studied not only at the syntactical level, or the topological level but in terms of semantic categories like cospan(multigraphs/G) (see [2]). I wanted to be able to model the hardware in my office with the tangle of wires connecting.
A technical matter I did not mention is that the category whose objects are finite sets, and whose arrows are cospans of groups between the free groups on these sets, has a subcategory with a braided monoidal structure, with a self dual structure on the objects, which I more or less described, but is quite different from the usual one we use on cospan(C) for C a category with finite colimits. (9/3/2011: Notice that in the original posting I claimed erroneously that the whole of the category was braided monoidal - the error was pointed out to me by Aurelio Carboni).
I almost forgot to explain the title. The advantage of the algebraic expression in cospan(groups) is that it is an open expression which may be evaluated and composed repeatedly. To deal only with knots or the closure of braids is like writing an operating system as a straight line program with a loop only at the end. It could be done (a theorem of Kleene) but it would be a crazy exercize. Programs are written by nested loops.
Coming back to John Armstrong. By googling cospans and knots I found two papers: one, The Extension of Knot Groups to Tangles [6], in which he defines topologically a cospan of groups to a tangle (he seems to have re-invented cospans himself for the purpose); the other [7] in which he describes algebraically a cospan of quandles to a tangle. (I don't feel so bad about not knowing John's work since he doesn't know about ours - a google search of cospans finds our papers on the second page. I guess we never figure in the n category cafe!)
I must admit that I haven't followed the enormous literature on the connection between geometry and monoidal categories even though I made some small contributions (i) with Carboni and Lawvere in 1983 - a lecture to the Sydney Category Seminar suggesting that symmetric monoidal categories should be thought of a categories with two monoidal structures analogously to the Eckmann-Hilton argument (Ross Street corrected this idea discovering braided monoidal categories with Andre Joyal) and (ii) the discovery with Carboni of the Frobenius equations in 1987.
[1] P. Katis, N. Sabadini, R.F.C. Walters, Span(Graph): an algebra of transition systems, Proceedings AMAST '97, SLNCS 1349, 322-336, 1997
[2] R. Rosebrugh, N. Sabadini, R.F.C. Walters, Calculating colimits compositionally, Montanari Festschrift, LNCS 5065, pp. 581–592, 2008.(also arXiv:0712.2525)
[3] L. de Francesco Albasini, N. Sabadini, R.F.C. Walters, Systems with discrete geometry, ART 2008, Analysing Reduction systems using Transition systems, 122--131, Forum, Udine, 2008.
[4] P. Katis, N. Sabadini, R.F.C. Walters, On the algebra of systems with feedback & boundary, Rendiconti del Circolo Matematico di Palermo Serie II, Suppl. 63 (2000), 123-156
[5] L. de Francesco Albasini, N. Sabadini, R.F.C. Walters, Cospans and spans of graphs: a categorical algebra for the sequential and parallel composition of discrete systems, arXiv:0909.4136
[6] John Armstrong, The Extension of Knot Groups to Tangles,http://arxiv.org/pdf/math/0509665
[7] John Armstrong, Categorifying Coloring Numbers, http://arxiv.org/pdf/0803.1642
The idea is to see a knot as a system composed from parts. Let's look at the trefoil:
The components which we wish to use to build knots are the following:
Finally, the knot group is the free group on all the letters quotiented by the equations.
In the case of the trefoil, if we express all the letters in terms of "a" and "e" the equations reduce to one equation, namely "aea=eae", so the knot group is ‹ a,e; aea=eae› .
Notice the resemblance to, for example, analogue circuit diagrams where we associate voltages and currents to the wires and differential equations to the components (see [3,4])
So what are we doing here? The letters on the wires entering (or leaving a component) may be thought of as the generators of a free group. The equation in the middle of a component may be thought of a the quotient of the coproduct of the input and output free groups defined by the relations. So a component is a cospan of groups between free groups. The whole diagram is a tensor diagram in Groups (the tensor being +) and the knot group is its tensor colimit as described in [2]. As described in [2] this colimit may be calculated by evaluating an expression in the monoidal category of cospans of groups.
For the trefoil, the expression is (C+C)*(1+S+1)*(1+1+Z)*(1+S+1)*(D+D) (+ means coproduct, * means composition).
Notice that a cospan of groups is assigned to any meaningful expression, that is to any tangle, not just to closed knots. The cospan corresponding to a braid is Artin's representation of a braid as an automorphism of a free group.
One of the motives for these thoughts were the remarks I made in an earlier post that graphical languages should be studied not only at the syntactical level, or the topological level but in terms of semantic categories like cospan(multigraphs/G) (see [2]). I wanted to be able to model the hardware in my office with the tangle of wires connecting.
A technical matter I did not mention is that the category whose objects are finite sets, and whose arrows are cospans of groups between the free groups on these sets, has a subcategory with a braided monoidal structure, with a self dual structure on the objects, which I more or less described, but is quite different from the usual one we use on cospan(C) for C a category with finite colimits. (9/3/2011: Notice that in the original posting I claimed erroneously that the whole of the category was braided monoidal - the error was pointed out to me by Aurelio Carboni).
I almost forgot to explain the title. The advantage of the algebraic expression in cospan(groups) is that it is an open expression which may be evaluated and composed repeatedly. To deal only with knots or the closure of braids is like writing an operating system as a straight line program with a loop only at the end. It could be done (a theorem of Kleene) but it would be a crazy exercize. Programs are written by nested loops.
Coming back to John Armstrong. By googling cospans and knots I found two papers: one, The Extension of Knot Groups to Tangles [6], in which he defines topologically a cospan of groups to a tangle (he seems to have re-invented cospans himself for the purpose); the other [7] in which he describes algebraically a cospan of quandles to a tangle. (I don't feel so bad about not knowing John's work since he doesn't know about ours - a google search of cospans finds our papers on the second page. I guess we never figure in the n category cafe!)
I must admit that I haven't followed the enormous literature on the connection between geometry and monoidal categories even though I made some small contributions (i) with Carboni and Lawvere in 1983 - a lecture to the Sydney Category Seminar suggesting that symmetric monoidal categories should be thought of a categories with two monoidal structures analogously to the Eckmann-Hilton argument (Ross Street corrected this idea discovering braided monoidal categories with Andre Joyal) and (ii) the discovery with Carboni of the Frobenius equations in 1987.
[1] P. Katis, N. Sabadini, R.F.C. Walters, Span(Graph): an algebra of transition systems, Proceedings AMAST '97, SLNCS 1349, 322-336, 1997
[2] R. Rosebrugh, N. Sabadini, R.F.C. Walters, Calculating colimits compositionally, Montanari Festschrift, LNCS 5065, pp. 581–592, 2008.(also arXiv:0712.2525)
[3] L. de Francesco Albasini, N. Sabadini, R.F.C. Walters, Systems with discrete geometry, ART 2008, Analysing Reduction systems using Transition systems, 122--131, Forum, Udine, 2008.
[4] P. Katis, N. Sabadini, R.F.C. Walters, On the algebra of systems with feedback & boundary, Rendiconti del Circolo Matematico di Palermo Serie II, Suppl. 63 (2000), 123-156
[5] L. de Francesco Albasini, N. Sabadini, R.F.C. Walters, Cospans and spans of graphs: a categorical algebra for the sequential and parallel composition of discrete systems, arXiv:0909.4136
[6] John Armstrong, The Extension of Knot Groups to Tangles,http://arxiv.org/pdf/math/0509665
[7] John Armstrong, Categorifying Coloring Numbers, http://arxiv.org/pdf/0803.1642
Labels: category theory, Como Category Seminar, computing, mathematics
posted by Unknown at 8:09 AM
1 Comments:
To be fair, I don't know about much work anymore, having failed to make any traction in the academic market. If you can take these ideas and find someone willing to hire you to pursue them, great. Nobody wanted to hire me to do it.
Post a Comment
<< Home