Categorical algebras of relations
(i) the notion of allegory of Peter Freyd and Andre Scedrov;
(ii) the notion of bicategory of relations of Aurelio Carboni and myself.
These two notions begin with the idea that relations form the arrows of a category Rel, and more that the order between relations induces a 2-category structure on Rel.
That is, given relations $R:X\to Y$, $S:Y\to Z$ (i.e. $R$ a subset of $X\times Y$, $S$ a subset of $Y\times Z$) denote the composite as $R\circ S$; then composition is associative and has an identity. Further $R\subset T:X\to Y$, $S\subset U:Y\to Z$ implies that $R\circ S\subset T\circ U$.
After this common beginning the two notions diverge. The definitions take different operations and constants, and as a result the axioms are quite different. I don't want to go into all the details but concentrate on one particular aspect.
Allegories take as operations a) the intersection of relations $R\cap T:X\to Y$, and b) the opposite $R^{o}$ of a relation $R$. Then the main axiom is the modular law, namely that
\[(RS\cap T)\subset (R\cap TS^{o})S.\]
Bicategories of relations instead take as operations $R\times S:X\times Y\to Z\times W$, and
$\Delta :X \to X \times X$, and $\nabla :X \times X\to X$
($\Delta$ is the diagonal relation whereas $\nabla$ is the opposite of the diagonal.)
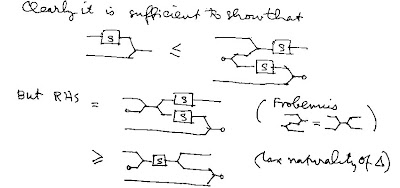
Among the axioms are the requirement that $\Delta_X$ and $\nabla_X$ are the commutative comultiplication and multiplication of comonoid and monoid structures on $X$ and that $\Delta_X$ and $\nabla_X$ are lax natural; that is, $R\Delta\subset \Delta(R\times R)$ and $\nabla R\subset (R\times R)\nabla$.
But the main axioms are the so-called Frobenius equations:
\[(1\times \Delta)(\nabla\times 1)=\nabla\Delta,\]
\[(\Delta\times 1)(1\times\nabla)=\nabla\Delta,\]
and the separable axiom
\[\Delta\nabla =1.\]
(which first occur in our work).
It is immediately clear that there is a difference between the notions - allegories have no operations on objects and hence are likely to be more common. However our claim is that bicategories of relations are more natural. This is supported by the fact that subsets of our axioms are satisfied by many other naturally occuring examples, like 2D topological field theories, etc etc. The Frobenius axiom seems to be turning up all over the place. It is essentially an axiom of equality. We think the modular axiom is a trifle bizarre.
What I would like to do in this post is to explain why our axioms imply the modular law, exhibiting at the same time the graphical language of bicategories of relations.



Peter Johnstone missed an opportunity in the chapter on allegories in his book "Sketches of an elephant", Oxford University Press, 2002..
Some people however like the bizarre in mathematics. I think the modular law is an example of "formiche mentali".
Labels: category theory, computing, mathematics
