Categorical algebras of relations

I would like to discuss two different algebras of relations:
(i) the notion of allegory of Peter Freyd and Andre Scedrov;
(ii) the notion of bicategory of relations of Aurelio Carboni and myself.

These two notions begin with the idea that relations form the arrows of a category Rel, and more that the order between relations induces a 2-category structure on Rel.

That is, given relations $R:X\to Y$, $S:Y\to Z$ (i.e. $R$ a subset of $X\times Y$, $S$ a subset of $Y\times Z$) denote the composite as $R\circ S$; then composition is associative and has an identity. Further $R\subset T:X\to Y$, $S\subset U:Y\to Z$ implies that $R\circ S\subset T\circ U$.

After this common beginning the two notions diverge. The definitions take different operations and constants, and as a result the axioms are quite different. I don't want to go into all the details but concentrate on one particular aspect.

Allegories take as operations a) the intersection of relations $R\cap T:X\to Y$, and b) the opposite $R^{o}$ of a relation $R$. Then the main axiom is the modular law, namely that
\[(RS\cap T)\subset (R\cap TS^{o})S.\]

Bicategories of relations instead take as operations $R\times S:X\times Y\to Z\times W$, and
$\Delta :X \to X \times X$, and $\nabla :X \times X\to X$
($\Delta$ is the diagonal relation whereas $\nabla$ is the opposite of the diagonal.)

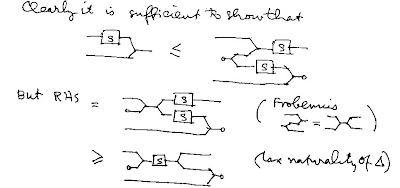
Among the axioms are the requirement that $\Delta_X$ and $\nabla_X$ are the commutative comultiplication and multiplication of comonoid and monoid structures on $X$ and that $\Delta_X$ and $\nabla_X$ are lax natural; that is, $R\Delta\subset \Delta(R\times R)$ and $\nabla R\subset (R\times R)\nabla$.
But the main axioms are the so-called Frobenius equations:
\[(1\times \Delta)(\nabla\times 1)=\nabla\Delta,\]
\[(\Delta\times 1)(1\times\nabla)=\nabla\Delta,\]
and the separable axiom
\[\Delta\nabla =1.\]
(which first occur in our work).
It is immediately clear that there is a difference between the notions - allegories have no operations on objects and hence are likely to be more common. However our claim is that bicategories of relations are more natural. This is supported by the fact that subsets of our axioms are satisfied by many other naturally occuring examples, like 2D topological field theories, etc etc. The Frobenius axiom seems to be turning up all over the place. It is essentially an axiom of equality. We think the modular axiom is a trifle bizarre.

What I would like to do in this post is to explain why our axioms imply the modular law, exhibiting at the same time the graphical language of bicategories of relations.






Peter Johnstone missed an opportunity in the chapter on allegories in his book "Sketches of an elephant", Oxford University Press, 2002..

Some people however like the bizarre in mathematics. I think the modular law is an example of "formiche mentali".

Jobs for mathematics graduates

Recently I have spoken to several Italian high-school teachers. Their advice to students proceeding to university is that the important thing is to do something you like. This seems to me to be dangerous advice. It is important not to do something you don't like, if possible. However, a student must consider future job prospects in making a decision. It is no good training for non-existing positions and then demanding that the positions be created afterwards. It is not reasonable to imagine that it is trivial to change after spending three or more years learning skills in one area - this is to discount the value of education. One should realize also that educators in an area have an interest in attracting students independent of job opportunities.

Contrast the following two documents: one is the advice of the Mathematics Department, New York University; the other is a blog by a mathematics graduate:

Mathematics Department, New York University
"Career Opportunities
The study of mathematics can lead to a variety of exciting professional careers. Basic research, engineering, finance, business, and government service are among the opportunities open to those with mathematical training. Moreover, with the increasing importance of basic science and information technology, prospects for careers in the mathematical sciences are very good. Mathematical analysis and computational modeling are important for solving some of the most pressing problems of our time - new energy resources, climate change, risk management, epidemiology, to name a few. We must strive to maintain our technological edge; mathematical skills will be crucial to this effort.
Some more specific business positions include portfolio analysis, design studies, statistical analysis, computer simulation, software design and testing, and other areas of operations research. There are extensive opportunities for mathematics in finance, the actuarial fields, and economic forecasting.
Many laboratories, both government and private, maintain independent research staffs that include mathematicians. Their work often deals with the development of new technology, including research in basic physics and software development, as well as applied mathematics. Numerical simulation, such as weather and climate forecasting, depends heavily on the use of supercomputers.
Practical considerations aside, there is the pleasure of learning, applying, and creating mathematics. Real world issues pose problems that can be studied by formulating and analyzing mathematical models. In some cases applications may lead to new mathematics, and a new branch of the science is born. In other cases abstract theory finds unexpected practical purpose. Working on research problems is exciting; solving difficult problems successfully is, for many, satisfaction enough."

John Armstrong's blog
"All the evidence I see is that mathematics, in and of itself, is worthless in the current job market. It seems to have value solely as training in addition to some other primary field of study. I would love to be proven wrong, but every rejection (most without comment) that passes reinforces this hypothesis."

Update The comment by Sean Carmody that follows is interesting. When a new area which needs mathematical expertize opens there may be opportunities for people with only mathematical degrees but for a limited time. Unfortunately the advice given to new students doesn't mention the limited time, just the successes. I had a similar experience: when I finished a masters degree in mathematics in 1966 (?) I looked at job opportunities. Programming was open to anyone. Now a mathematics student without programming experience has to compete with people with years of experience for such positions.

Trouble at n-category cafe

One of the blogs I look at rather regularly is n-category cafe. A recent post Math: Folk Wisdom in an Electronic Age raises questions about the future of mathematical discussion on the web.

There seems to have developed contrasting opinions among the presenters of the blog. In brief, one group holds that blogs should be entertaining as well as informative. The other group has more serious intentions.

I think there is a place for entertaining blogs which at the same time inform. However there should be a clear separation between this level of discussion and precise scientific papers.

The danger from the entertainers' direction is that papers try to be entertaining and lose precision.

The danger from the serious bloggers is that serious-sounding blogs take the place of papers, while being pretentious but not precise.

A paper or a book is a concentrated form of knowledge which cannot be replaced by conversations. A paper or a book can be helped by the addition of informal discussion.

University reform in Italy

I have written several times, always as a foreigner trying to understand the Italian mind, about university reform. I think however I have not emphasized an important (perhaps the most important) aspect. What follows is my imperfect understanding.

Money comes the the universities for two reasons - from research applications, and from the student enrolment.

Research money is fickle and allows one to employ temporary staff. (Research staff and graduate students are of course almost essential for certain areas of research.)

Student money is hard, and allows one to employ permanent staff. The desire to employ permanent staff in ones area seems to be a main driving force for Italian (maybe all) academics.

So what did Italian academics do in recent years? Create courses to attract students. Insubria university in Como created in Science an Informatica course and a Bene Culturale course. In Giurisprudenza the university created Scienze di Turismo and Mediazione Linguistica. These courses did attract students.

However the resulting money coming to the university from student numbers was used, not for permanent staff in the new areas, but for staff in the old areas.

With the contraction of the reform these new courses may/must close for lack of staff, with a resulting loss of a large proportion of the student numbers.

Megatrends

I learnt the word megatrend listening to a talk of Federico Faggin in Milano a few years ago. Federico Faggin has his initials on the first microprocessor ever produced (Intel 4004). He also founded Zilog with Ungermann, and designed the Z80. And other things. So perhaps he has the right to talk of megatrends.

I think one of the megatrends of the 20th and perhaps 21st century is the use of computers in almost every phase of life, in particular for communication. It is perhaps comparable to the industrial revolution, and is changing the work people do in a similarly dramatic fashion.

Universities however seem to be rather bad at adjusting to megatrends. A professional academic is happy at new and exciting developments in his/her field, but new areas are invisible.

The University of Insubria seems to be just in the process of closing a Laurea in Informatica in Como. With the reform it seems to be the only possibility acceptable to the physicists, mathematicians, chemists and ambientalists, in particular as a result of the lack of investment of the Como Faculty of Science in Informatica over a period of some years. Fortunately it is likely there will be a laurea in informatica in Varese, but with a small investment in Informatica over the years, instead of losing the course in Como, the University could have had courses in both Como and Varese.

I think the lack of investment in Informatica has been a megamistake for Como.

New paper with Steve Lack and Richard Wood - bicategories of spans

We have just put a new paper on arxiv called "Bicategories of spans as cartesian bicategories", where we characterize such bicategories as follows: a bicategory is biequivalent to Span(E) for E a category with finite limits iff it is cartesian, each comonad has an Eilenberg-Moore object, and every map is comonadic.

There is quite a bit of further stuff in the paper, but one extra point I would like to mention as it is relevant to our paper on spans and cospans.

The extra result is that Span(E) for E finitely complete has direct sums iff E is extensive. This is related to work of Heindel and Sobocinski (T. Heindel and P. Sobocinski. Van Kampen colimits as bicolimits in Span. In Calco '09, LNCS, Springer, 2009).

To bring this result down to earth lets look at Span(Sets) and see why it has direct sums. Consider a span R from X to Y. Suppose X=U1+U2+..Um, and Y=V1+...Vn. Then clearly R breaks up into a family of sets Rij, the elements which go from Ui to Vj. So the span R becomes a matrix Rij of spans. A special case of this is when R is an endomorphism of X, that is, R is a graph. If the vertices of the graph break up as a sum U1+...Um, the graph may be expressed as a square matrix of spans Ui->Uj (i,j=1,2,...,m). (A span in sets is a kind of bipartite graph.)

On names

Recently I have been thinking about the importance of standardizing definitions and names in Science.

I was looking at the notion of regular category, which is the correct setting for defining relations. Unfortunately this important concept has not settled completely. A regular category in the first place is finitely complete. But then some papers assume the existence of all coequalisers, but most (correctly) prove the existence of coequalisers of kernel pairs from a factorization system into extremal epis and monos, plus the fact that extremal epis are preserved by pullback (Joyal).

Unfortunately what I just called extremal epis are sometimes called strong epis or even special epis. Peter Johnstone in his Elephant book (which has a rather good treatment of regular categories) introduces another concept namely covers.

My point is that such a basic and important concept should not have a confusion of names or definitions.

However I really wanted to talk about a much more difficult problem, the naming of concepts in computer science.
The problem arises from two sources. One is that different forms of a concept have arisen in many different fields, and hence there are many existing names, usually with resticted sense, and hence difficult to use in an extended sense, with out upsetting the existing use. The second problem is confusion - the concepts have not been sufficiently analysed or a single name is used for several different concepts.

I could give a long list of examples. Let's take a few names and try to untangle them. The names I have in mind are "concurrent", "process", "system", "processor", "machine", "agent", "automaton".

Concurrent: the word appears to signify entities or behaviours of entities (two different things already) which run together, at the same time. In fact, the word has come to refer to, not entities, but behaviours which do not run together, but interleave.

Process: it is not clear in the literature whether process refers to an entity, or an entity in a state, or the behaviour of an entity. These are such fundamentally different things that they can't be confused.

System: the word system is so vague that it is difficult to use - but in the end we have resorted to using it in a recent paper. At least it is clear that a system is an entity.

Processor: is clearly an entity but seems to refer to a hardware component, so is insufficiently abstract.

Machine: similarly.

Agent: seems to be an entity but is used by many (Milner) to mean a process in a certain state (and what is a process?).

Automaton: seems like a good word for an entity, but a difficulty is that the word either is used in a very limited meaning (by finite state automata theorists) or there are too many uses for the word.

One more word, rather different. The word "series" has long been used in electrical circuit theory to denote a system physically constructed by a sequence of components. It does not mean that the behaviour is sequential although if the circuit contains pulses it may be. We used in at least one paper the word series composition to mean "communicating parallel composition" as it does in such circuits. I think we were mistaken to do so because series certainly suggests "sequential", which we definitely did not intend.

The nerve of n-category - with Michael Johnson 1987

I see a recent post on n-category cafe explaining higher dimensional associativities. There is no reference to Ross Street's orientals (Ross Street, The algebra of oriented simplexes , J. Pure Appl. Algebra 49 (1987) 283-335; MR89a:18019) of twenty odd years ago. An old paper of mine with Michael Johnson might also be of some interest.

One of the effects of blogging is a certain loss of history, which is also a loss of content. Formal papers have always made some attempt at recording the history of ideas. I think blogging might well benefit from some increased formalism, since it seems inevitably to be taking over dissemination of research.

On cospans and spans II

A little explanation of the paper http://arxiv.org/abs/0909.4136.

The aim of the paper is to describe discrete systems which communicate in parallel (that is, they are distributed in space) and evolve sequentially (the physical form of the system may change). This is an aim shared with so many (prior) authors it is invidious to begin a list but I must do so - Milner, Hoare, Petri, Zielonka, Nivat, ...

The basic model we take for a system is a graph of states and transitions.

To be capable of being combined with others a system must have borders, boudaries, or interfaces. Two types of interfaces are necessary. The first are sequential interfaces, drawing inspiration from the sequential operations of Kleene. A system must have (generalized) initial and terminal states. We commence more generally with two graph morphisms into the system.

A system with sequential interfaces is a cospan
\[\usepackage[all]{xy}\xymatrix{
A\ar[r]^{\gamma_{0}}& G&B \ar[l]_{\gamma_1}
}\]
of graphs. The graph $G$ is the graph of the system; $A$, and $B$ are the graphs of the interfaces. Systems compose sequentially by pushout.

For the parallel interfaces we take inspiration from the model of circuits. Circuits have transitions which are reflected on the boundaries. We take here as our definition two graph morphisms out of the system

A system with parallel interfaces is a span
\[\usepackage[all]{xy}\xymatrix{
X& G\ar[l]_{\partial_{0}}\ar[r]^{\partial_{1}}&Y
}\]
of graphs. The graph $G$ is the graph of the system; $X$, and $Y$ are the graphs of the interfaces. Parallel composition of systems is by pullback.

A system with sequential and parallel interfaces consists of a
commutative diagram of graphs and graph morphisms
\[\usepackage[all]{xy}
\xymatrix{
G_0\ar[d]_{\gamma_0} & X \ar[l]_{\partial_0}\ar[d]_{\gamma_0}\ar[r]^{\partial
_1}&G_1\ar[d]_{\gamma_0}\\
A & G\ar[l]_{\partial_0} \ar[r]^{\partial_1}&B\\
G_2\ar[u] ^{\gamma_1}& Y\ar[l]_{\partial_0}\ar[u]^{\gamma_1}\ar[r]^{\partial
_1}&G_3\ar[u]^{\gamma_1}}%
\]

We denote such a system very briefly as $G_{Y;A,B}^{X}$, or even $G_{Y}^{X}$
or $G_{A,B}$ or even just $G$, depending on the context.

Aesop on the importance of having decisive leadership

Living in Italy, in particular working in Italian academia, makes one think frequently of the problem of good government. There are famous frescoes of Lorenzetti in the Comune di Siena called "ALLEGORIA DEL BUONO E CATTIVO GOVERNO".

We are now at a critical point in the University of Insubria in the discussion of University reform. It looks as if we may finally have to implement the 25% reduction in courses proposed by the minister (for universities which until now had the minimum number of teachers) - though Italians tell me that I am naive to imagine such a definite result. Some of us believe that decisive leadership is crucial at this time. I would prefer wise leadership. Maybe even benevolent leadership.

I suppose that is also naive. Consider the following story.


THE FROGS WHO WISHED FOR A KING

The Frogs were tired of governing themselves. They had so much freedom that it had spoiled them, and they did nothing but sit around croaking in a bored manner and wishing for a government that could entertain them with the pomp and display of royalty, and rule them in a way to make them know they were being ruled. No milk and water government for them, they declared. So they sent a petition to Jupiter asking for a king.

Jupiter saw what simple and foolish creatures they were, but to keep them quiet and make them think they had a king he threw down a huge log, which fell into the water with a great splash. The Frogs hid themselves among the reeds and grasses, thinking the new king to be some fearful giant. But they soon discovered how tame and peaceable King Log was. In a short time the younger Frogs were using him for a diving platform, while the older Frogs made him a meeting place, where they complained loudly to Jupiter about the government.

To teach the Frogs a lesson the ruler of the gods now sent a Crane to be king of Frogland. The Crane proved to be a very different sort of king from old King Log. He gobbled up the poor Frogs right and left and they soon saw what fools they had been. In mournful croaks they begged Jupiter to take away the cruel tyrant before they should all be destroyed.

"How now!" cried Jupiter "Are you not yet content? You have what you asked for and so you have only yourselves to blame for your misfortunes."

Steve Lack wins the Australian Mathematical Society Medal.

I am very pleased to hear the news that Steve Lack has won an Australian Mathematical Society Medal this year.

He did his fourth year essay in Sydney with me on extensive categories (my interest arose from the use of distributive and extensive categories in Computer Science). I think however he learnt much more about the way of doing mathematics from Max Kelly. He seems to have Max Kelly's great style of clarifying and solving problems. He went on to do his PhD with Peter Johnstone in Cambridge. As I commented in a post I enjoyed his talk perhaps the most in Capetown this year.

One interesting aspect of the award was that Category Theory seems almost to have joined the main stream. I remember some years ago when Gus Lehrer prophesied that there would not be any more posts for category theorists at the University of Sydney - and after I left Sydney, and until now, this prediction seems to have been fulfilled. We can hope that maybe in the future category theory might return to the University of Sydney where it flourished for so many years, and gave such credit to the university.